MinHash Based Fuzzy Match on Graph

Many graph use cases require fuzzy matching, a method used to find similar, but not exactly matching, phrases in a database. Some examples of fuzzy matching include inputting a string of characters, searching records with similar string attribute values, or finding a set of data records that have similar string values. Fuzzy matching is valuable in entity resolution, where data like first and last names needs to be identified and matched. In anti-fraud use cases, fuzzy matching can be used to match unstandardized addresses on credit card applications.

In a graph data structure, performing string fuzzy matches is challenging because:

• With the graph data structure, it’s simple to perform an exact match with vertices created using the string values as their ID; however, it’s challenging to introduce a connection for a fuzzy match
• Introducing additional components to the architecture using some indexing and search engines would solve the problem. This approach increases the system maintenance workload and the complexity of updating and querying the data.

By utilizing the MinHash approach during the graph loading process, vertices with similar string attribute values can be indirectly connected through common intermediary vertices whose IDs are the MinHash signature values. This approach has the following advantages:

1. It doesn’t rely on additional architecture
2. Performance is maintained by only scanning the relevant vertices without having to scan a large population of vertices
3. Values are stored natively in the graph database in the form of vertices and edges, so the required data structure is automatically partitioned and distributed
4. Search is done through graph traversal, which means we can adopt different algorithms to evaluate the string distance. 
5. All searches are automatically parallelized.

What is MinHash?

MinHash is a technique for evaluating string similarities. MinHash can reduce each string into fixed dimensions, which is a set of MinHash signatures. By calculating the Jaccard Similarity of the MinHash signature sets of different strings, we can get the string similarity. 

It takes the following steps to calculate the MinHash Signatures:

1. Calculate the k-shingle of a given size k of a string. The k-shingle of a string is all possible consecutive substrings of length k. For example, the k-shingle with k value equals 4 of string, “James Smith” is {“Jame”, “ames”, “mes ”, “es S”, “s Sm”, “ Smit”, “mith”}
2. Hash each substring into j integer hash codes with j different hash functions. For example, if j equals 4:
   
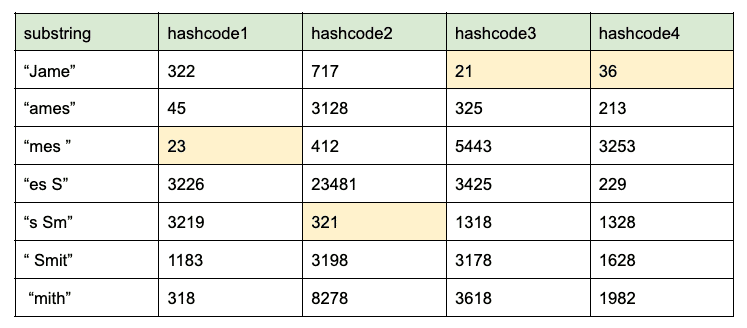
3. The set minimum hashcode value for each hash code is 23, 321, 21, and 36. Therefore, the MinHash signature of string “James Smith” is {23, 321, 21, 36} 

How Does MinHash Work on Graph?

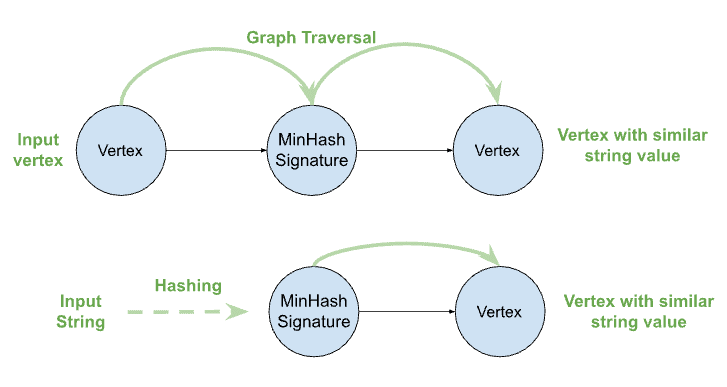
In the graph-based solution, for any given strings that will be used for the fuzzy match, we will first calculate the MinHash signatures, then create vertices using the Minhash signatures as the vertex ID. From there, we’ll connect the vertices that own the string values to those corresponding MinHash signature vertices.

This way, the MinHash signature vertices can be used to match the vertices having similar string values. For example, given a vertex, to find the vertices with similar string values, we just need to traverse to the intermediary MinHash signature vertices first, then from the MinHash signature vertices to the other connected vertices. This way without having to scan all the vertex populations, the vertices with similar string values can be found through graph traversal through the Minhash signature vertices.

In the same way, we can also convert any input string into MinHash signatures to allocate the MinHash signature vertices in order to find the vertices with similar string values to the input string.

The Workflow on TigerGraph

TigerGraph is a massively parallel processing graph analytical platform. Implementing the MinHash fuzzy match on TigerGraph is possible by taking the following steps.

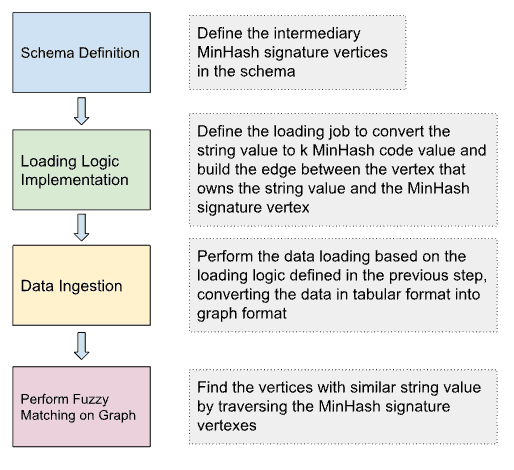
Schema Definition

In the graph schema, define the vertex type for MinHash signature and edge type between the entity that owns the string attribute and the MinHash signature vertex.

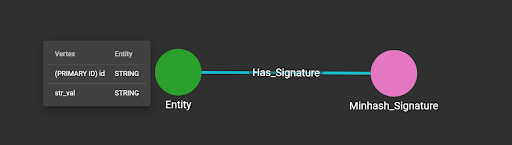
Loading Jobs

The loading job converts the strings to be matched into k MinHash signatures values, the number k is a configurable number of hash functions that will be used in the MinHash process. To do this, a TokenBank function is used. The complete tokenbank.ccp file can be found here.

The input to the TokenBank function is the string value for the fuzzy matching and the value of k and j. In our example, k=3 and j=10. The output of the TokenBank function is the MinHash signature delimited by “|”. With the output, the flatten function of the loading job is used to load the split string into a temp_table.

PUT TokenBank FROM "TokenBank.cpp"

use graph MinHash
drop job load_hash
CREATE LOADING JOB load_hash FOR GRAPH MinHash {
      DEFINE FILENAME MyDataSource;
      LOAD MyDataSource TO TEMP_TABLE t1(vertexID, signature, stringvalue) VALUES($0, FLATTEN(minHash($1,"3","10"), "|", 1), $1) USING SEPARATOR=",", HEADER="false", EOL="\n";
      LOAD TEMP_TABLE t1 TO EDGE Has_Signature VALUES($"vertexID", $"signature"),
                         TO VERTEX Entity VALUES($"vertexID", $"stringvalue");
}

run loading job load_hash using MyDataSource="data.csv"

By executing the script above, the data below is ingested.

1,TigerGraph
2,Tiger Grph
3,TiiigerGraph
4,Sheila M. Swinton
5,Sheila Swinton
6,Beverly Farmer
7,Bev Farmer
8,Crystal Pablo
9,Chrissy Pablo

Data Loading

By running the loading jobs, the edges between the entity that owns the string attribute and the MinHash signatures of the string value are connected. Below are the visualization results from the Explore Graph page.

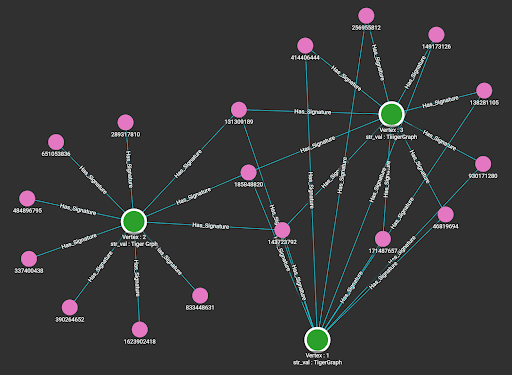
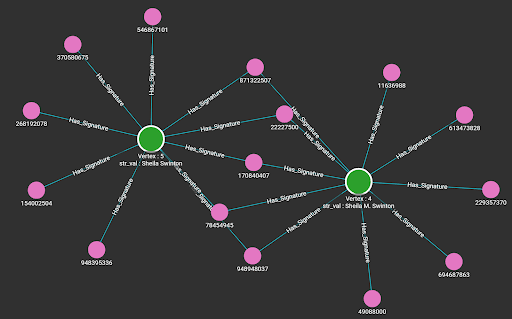
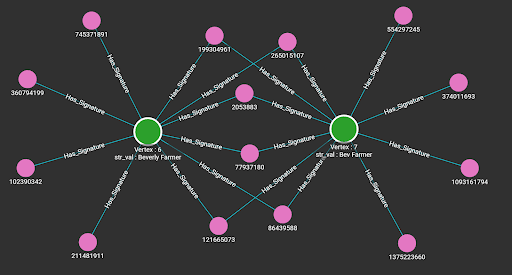
Queries

To perform the fuzzy match between vertices, either apply Jaccard Similarity or directly use the Jaro–Winkler distance expression function. The Jaccard Similarity approach will calculate the topological similarity based on the number of common MinHash signature vertices between the vertices to be matched. Because we only have a limited number of MinHash signatures, the result of the Jaccard Similarity will be approximate. To obtain an accurate string similarity, the string distance function is recommended.

Below is the query utilizing the string distance function that takes a vertex as input and returns the vertices that have similar strings, ordered by the similarity.

CREATE QUERY string_distance(VERTEX input) FOR GRAPH MinHash { 

 SumAccum @similarity;
  STRING val;

 start = {input};

 signatures = SELECT t FROM start:s-(Has_Signature)-:t
                       POST-ACCUM val = s.str_val;

 matches = SELECT t FROM signatures:s-(Has_Signature)-:t
                   WHERE t != input
                   ACCUM t.@similarity += jaroWinklerDistance(val, t.str_val)
                    ORDER BY t.@similarity DESC;

 print matches;
}

Result when taking vertex 1 as input.

[
  {
    "matches": [
      {
        "attributes": {
          "@similarity": 9.55556,
          "str_val": "TiiigerGraph"
        },
        "v_id": "3",
        "v_type": "Entity"
      },
      {
        "attributes": {
          "@similarity": 2.88,
          "str_val": "Tiger Grph"
        },
        "v_id": "2",
        "v_type": "Entity"
      }
    ]
  }
]

Below is the single source Jaccard Similarity query from the Graph Data Science Library.

CREATE QUERY tg_jaccard_nbor_ss (VERTEX source, STRING e_type, STRING rev_e_type, 
 INT top_k = 100, BOOL print_accum = TRUE, STRING similarity_edge_type = "", STRING file_path = "")  SYNTAX V1 {

/*
Calculates the Jaccard Similarity between a given vertex and every other vertex.
 Jaccard similarity = intersection_size / (size_A + size_B – intersection_size)
Parameters:
source: start vertex                           top_k: #top scores to report
e_type: directed edge types to traverse        print_accum: print JSON output
rev_e_type: reverse edge types to traverse     file_path: file to write CSV output to
similarity_edge_type: edge type for storing vertex-vertex similarity scores

 This query current supports only a single edge type (not a set of types) – 8/13/20
*/

 SumAccum @sum_intersection_size, @@sum_set_size_A, @sum_set_size_B;
 SumAccum @sum_similarity;
 FILE f (file_path);

 Start (ANY) = {source};
 Start = SELECT s
   FROM Start:s
   ACCUM @@sum_set_size_A += s.outdegree(e_type);

 Subjects = SELECT t
      FROM Start:s-(e_type:e)-:t;

 Others = SELECT t
    FROM Subjects:s -(rev_e_type:e)- :t
    WHERE t != source
    ACCUM 
        t.@sum_intersection_size += 1,
        t.@sum_set_size_B = t.outdegree(e_type)
    POST-ACCUM 
        t.@sum_similarity = t.@sum_intersection_size*1.0/(@@sum_set_size_A + t.@sum_set_size_B – t.@sum_intersection_size)
    ORDER BY t.@sum_similarity DESC
    LIMIT top_k;

 IF file_path != “” THEN
     f.println(“Vertex1”, “Vertex2”, “Similarity”);
 END;

 Others = SELECT s
    FROM Others:s
    POST-ACCUM 
        IF similarity_edge_type != “” THEN
            INSERT INTO EDGE similarity_edge_type VALUES (source, s, s.@sum_similarity)
        END,
        IF file_path != “” THEN 
            f.println(source, s, s.@sum_similarity) 
        END; 

 IF print_accum THEN
     PRINT Others[Others.@sum_similarity];
 END;
}

Result when taking vertex 1 as input.

[
  {
    "Others": [
      {
        "attributes": {
          "Others.@sum_similarity": 0.17647
        },
        "v_id": "2",
        "v_type": "Entity"
      },
      {
        "attributes": {
          "Others.@sum_similarity": 1
        },
        "v_id": "3",
        "v_type": "Entity"
      }
    ]
  }
]

Below is the query that takes a query string as input, and returns the vertices that have a similar string value.

CREATE QUERY query_by_string(string query_str) FOR GRAPH MinHash { 
  
  SetAccum @@min_hash_signatures;
  SetAccum @@signatures_vertex;
  SumAccum @similarity;

@@min_hash_signatures = minHash(query_str,3,10);

@@signatures_vertex = to_vertex_set(@@min_hash_signatures, “Minhash_Signature”);

  start = @@signatures_vertex;

  start = SELECT t FROM start:s-(Has_Signature)-:t
            POST-ACCUM t.@similarity += jaroWinklerDistance(query_str, t.str_val)
            ORDER BY t.@similarity DESC;

  print start;
}

Below is the result of running the query above with input ‘tigergraph.’

{
    "start": [
      {
        "attributes": {
          "@similarity": 0.86667,
          "str_val": "TigerGraph"
        },
        "v_id": "1",
        "v_type": "Entity"
      },
      {
        "attributes": {
          "@similarity": 0.82222,
          "str_val": "TiiigerGraph"
        },
        "v_id": "3",
        "v_type": "Entity"
      },
      {
        "attributes": {
          "@similarity": 0.8,
          "str_val": "Tiger Grph"
        },
        "v_id": "2",
        "v_type": "Entity"
      }
    ]
  }

Conclusion

This blog introduced a way of running string fuzzy matches on graphs that is very performant, storage efficient, and easy to implement. The proposed approach doesn’t have to rely on additional infrastructure and can fulfill the need for both similar string value matching between vertices and fuzzy searching of vertex attribute values.

If you have any questions about this approach or using other graph algorithms or functions, we encourage you to join our TigerGraph Developer Community. On the community, you’ll find a collection of your peers, TigerGraph users from around the world, and our own graph experts, all of whom are committed to sharing their knowledge in an open, interactive forum.